量子力学是描述微观世界的物理学基石，它揭示了微观粒子可以“穿墙而过”（量子隧穿）、能量是离散的（能量量子化）等与经典物理学截然不同的奇特现象. 然而，一个由来已久的基本问题是：量子力学是否仅限于微观世界？为什么我们日常生活中由数十亿量级粒子组成的“宏观”物体不表现出这些量子特性？理论上，量子力学应该适用于任何系统，但对于包含大量粒子的宏观物体而言，其集体量子特性通常会因环境干扰（如热噪声）而迅速消失，即发生量子退相干. 因此，长期以来，人们普遍认为量子现象是微观系统的“专利”. 然而，物理学的魅力在于探索极限. 科学家们发现，大量微观粒子的集体效应，可以产生特殊的宏观量子物态，通过精确调节此宏观量子物态，可以观测到宏观层面的量子效应.

正是基于此，2025年诺贝尔物理学奖(下文简称“本次诺奖”)授予了三位美国物理学家: 约翰·克拉克、米歇尔·H·德沃雷和约翰·M·马蒂尼斯，以表彰他们“在电路中实现宏观量子力学隧穿效应和能量量子化”. 在四十年前完成的一系列工作中^[1~4]，他们巧妙地利用了超导中的集体量子态，成功地让一个由数十亿量级电子组成的电路系统，作为一个宏观整体展现出典型的量子特性. 例如，他们证明了电路的整体相位能够突破障碍进行隧穿，并且其能量是严格量子化的. 他们的实验证明，这种具有量子化能级的超导电路可以被精确控制，从而作为信息的承载单元——量子比特（Qubit）. 德沃雷和马蒂尼斯后来将这种电路发展成量子计算机的核心元件，为当前的超导量子计算技术路线奠定了基石. 三位获奖者的工作，相当于在实验室中成功制备了能展现量子行为的宏观系统，让“宏观量子相干性”成为了可测量、可利用的物理实体，让“薛定谔的猫态”不再只是思想实验. 他们的成果激励了全球科学家投入到利用宏观量子效应来开发新一代量子技术，包括更高精度的量子传感器和革命性的量子计算机. 这一发现不仅在物理学上打破了“量子效应仅限于微观”的传统观念，探索了量子效应产生的边界，更重要的是，它为人类利用宏观量子态提供了实验基础，开启了通往下一代量子科技时代的钥匙.

1

量子隧穿和能量量子化

在微观世界中，粒子遵循量子力学的基本原理而运动，运动的规律与我们日常经验中的经典物理规律截然不同，其中，量子隧穿和能量量子化是理解本次诺奖工作的两个核心概念. 在经典物理中，一个能量低于势垒高度的粒子，永远不可能穿过该势垒. 然而，在量子力学中，粒子由波函数描述，这使得粒子能有一定的概率穿过势垒，这就是量子隧穿现象. 介绍量子隧穿最基础的模型是一维方形势垒（1D square potential barrier）模型. 如图1所示，想象一道具有有限高度V₀和有限宽度L的“墙”，发出一个能量E<V₀的粒子射向这道墙，经典物理学预测这个粒子会被完全反射; 然而，量子力学的严格计算表明，粒子有非零的概率出现在“墙”的另一侧，仿佛茅山道士“穿墙而过”.

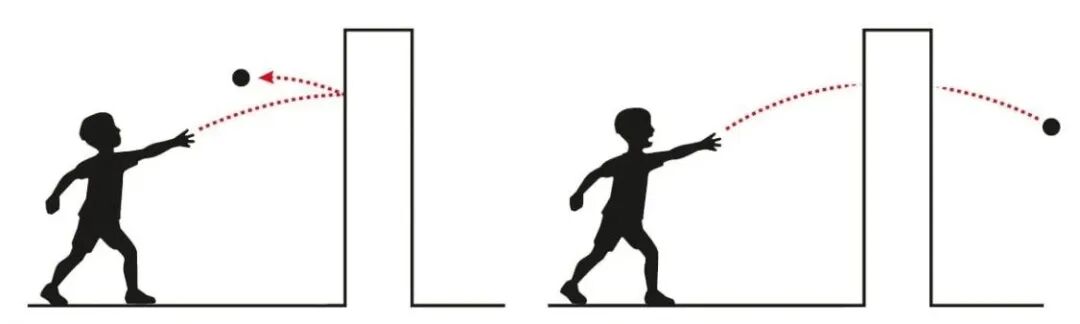
图1  一维方形势垒的说明图. 在经典的世界中，小球只会被墙面反射（左图），而遵循量子力学规律的小球会有一定概率“穿墙而过”（右图）. 图片来源: 链接

一个更一般的描述隧穿现象的模型，是一个有限深势阱的模型：想象一个粒子被困在一个深度和宽度都有限的单势阱中，这个势阱将粒子束缚在一个空间局域的区域，但同时存在一道有限高的势垒，在阱中处于束缚态的粒子，其能量只能取一系列离散的特定数值，被称为能级，这就是能量量子化现象. 尽管粒子被束缚在阱中，但其波函数也能延伸到势垒之外，因此，粒子具有非零的概率通过量子隧穿机制逃离势阱，进入未被束缚的自由状态. 事实上, 获得本次诺奖的三位科学家就是使用电流偏置约瑟夫森结，实现了这样一个宏观版本的“一维系统”，并且成功观察到了隧穿现象和能量量子化现象，如图2所示^[4].

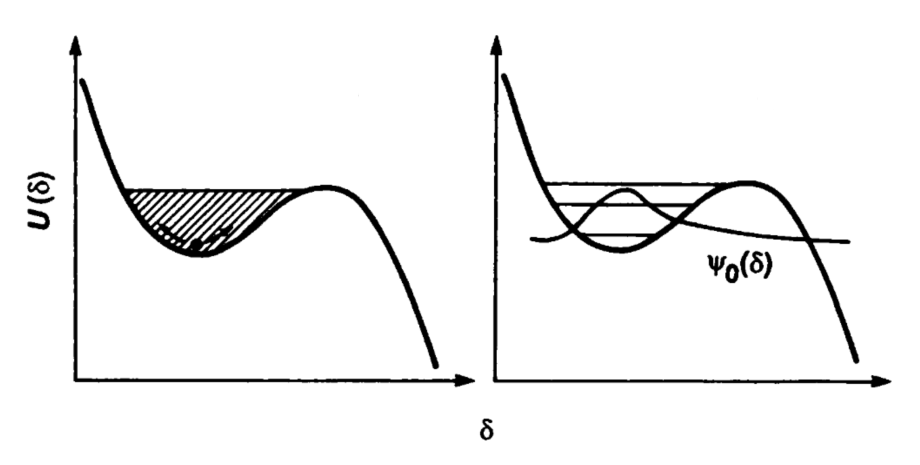
图2  处于束缚态粒子的局域波包能延伸到势垒之外^[4]

2

宏观量子态和宏观量子效应

第一节中描述的量子隧穿和能量量子化现象，都是原始的微观理论所揭示的规律. 然而，如果我们希望在由数十亿量级粒子构成的宏观世界中，实现第一节所描述的势垒和势阱，并且观察到对应的量子现象，应该如何实现呢？这就要从微观粒子的集体效应以及其导致的宏观量子态说起. 在通常的宏观物质中，单个微观粒子的量子特性会被无数次的散射和环境的干扰（热噪声）所淹没，导致量子退相干，因此宏观物体呈现出经典物理的行为. 然而，在某些极端条件下，例如极低的温度，粒子间的相互作用可以变得非常特殊，使它们不再是独立的个体，而是形成一种高度协同一致的集体行为. 这种集体行为，便是形成宏观量子态的关键. 比如，氦-4 (⁴He)原子是玻色子，当温度降到极低时，大量⁴He原子会“凝聚”到量子力学所允许的最低能量状态，形成玻色-爱因斯坦凝聚(BEC). 此时，所有原子拥有统一的、巨大的宏观波函数. 这个宏观波函数的行为，可以由宏观波动方程（格罗斯-皮塔耶夫斯基方程，G-P方程）来描述. 这种物质状态展现出完全无黏滞的流动（超流）^[5]，是典型的宏观量子现象. 又比如，固体中的电子是费米子，无法直接发生玻色-爱因斯坦凝聚. 但在极低温下，电子会两两配对，形成具有玻色子性质的“库珀对”. 随后，这些库珀对会像⁴He原子一样，凝聚到一个统一的量子态中. 此时，这些库珀对不再被视为独立粒子，而是作为一个庞大的整体行动. 这正是常规超导的微观产生机制, 此时整个系统拥有一个描述整个超导体的宏观波函数^[6].

事实上，这些宏观的量子物态背后已经与之前的一大批诺贝尔物理学奖产生了关联, 比如, 超流现象由苏联物理学家彼得·卡皮查最早于1937年发现, 他因此于1978年获得诺贝尔物理学奖; BEC最早的两位提出者萨特延德拉·玻色和阿尔伯特·爱因斯坦也是诺贝尔物理学奖得主; 2001年的诺贝尔物理学奖正是授予了最早通过实验在大量碱金属原子系统上实现BEC的三位物理学家: 埃里克·康奈尔、沃尔夫冈·克特勒和卡尔·威曼; 而发现常规超导的微观机制的三位科学家约翰·巴丁、利昂·库珀和约翰·施里弗也因此获得1972年的诺贝尔物理学奖.

将两块超导体（分别记为超导体1和超导体2）中间用一层极薄的绝缘体隔开，形成一个三明治结构. 英国物理学家布莱恩·约瑟夫森预言：尽管有绝缘层的阻隔，但是超导体中的库珀对依然可以通过微观量子隧穿过程，穿过绝缘层，从而形成无电阻的超导电流. 这种现象被称为约瑟夫森效应^[7]，约瑟夫森因此获得1973年的诺贝尔物理学奖. 这种结构被称为约瑟夫森结, 是一个非线性的且具有内在量子隧穿特性的宏观量子器件. 值得一提的是, 世界上第一个约瑟夫森结的制造者之一正是一代凝聚态物理大师, 1977年的诺贝尔物理学奖得主菲利普·安德森.

由于解释氦-3超流而获得诺贝尔物理奖的安东尼·莱格特分析了这个超导电路系统, 提出它可以实现宏观量子隧穿、宏观量子叠加等新奇物理效应^[8]. 正如前文所述，每块超导体都拥有一个宏观波函数Ψ，其可以表示为，其中ρ是库珀对的密度（幅度），而θ则是波函数的量子相位. 由于超导体内的所有库珀对都处于同一量子态，因此θ是一个描述整个宏观系统的物理量. 约瑟夫森相位(δ)正是这个宏观波函数在结两侧的相位之差

它是描述约瑟夫森结状态的核心宏观量子变量. 在不施加电压的情况下，超导电流的大小与相位差δ之间满足关系I=I₀sin(δ). 这里，I₀被称为约瑟夫森结的临界电流，是该结在不产生电压的情况下所能承载的最大超导电流. 约瑟夫森相位就像一个宏观粒子的“一维坐标”. 通过这种转化，整个超导电路系统被简化成了一个一维宏观量子系统.

通过向约瑟夫森结中注入一个直流偏置电流I_B，可以构造出如图3所示的一维势阱结构. 当电流偏置足够小时（I_B<I₀），这个势能像一个略微倾斜的、带有周期性小凹陷的斜坡. 我们只需要关注宏观变量δ在其中一个局部凹陷中的情况，这等效于图3(a)所示的情况，这时宏观相位就像一个在凹陷中停留的小球，势阱的底部对应于电路的零电压超导态.

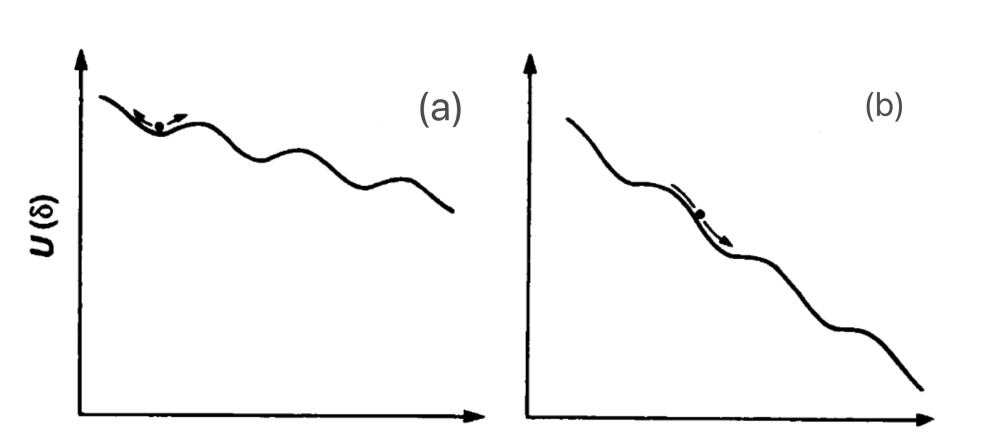
图3  一维相位空间中的势能图^[4]. (a) I_B<I₀; (b) I_B>I₀

获得本次诺奖的三位物理学家的一系列工作，正是基于这种特殊的偏置约瑟夫森结，通过精确的测量技术，首次证实了宏观量子隧穿和能量量子化：在极低温度下，三位科学家测量了系统从零电压态逃逸的速率，测量出的逃逸速率与量子隧穿理论预测的高度符合，证明了宏观相位δ像单个粒子一样，通过量子隧穿机制穿透势垒，而不是翻越势垒逃逸. 值得强调的是，这里的隧穿是在系统的广义坐标（相位）空间中发生的. 而I_B>I₀时，整个势能曲线不再有凹陷，宏观相位相当于在一个单调下降的斜坡上不断加速的小球，这时宏观量子效应不复存在，系统进入经典电阻态(图3(b)). 图4展示了偏置约瑟夫森结的示意图.

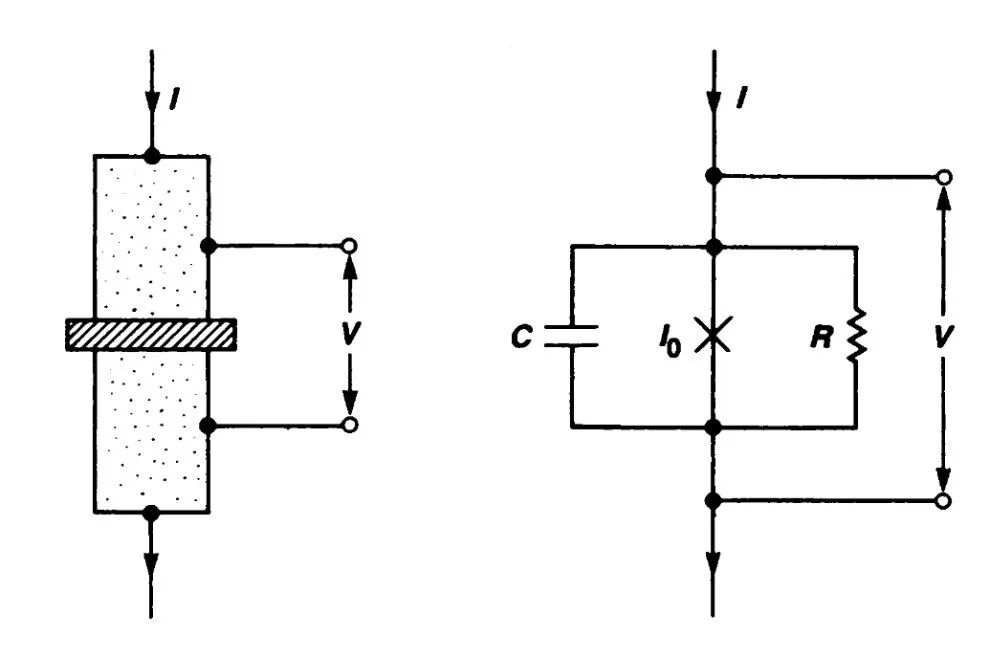
图4  偏置约瑟夫森结的装置图和实验的电路图^[4]

为了探测被束缚在势阱中的宏观相位是否具有离散能级，科学家们对系统进行了微波谱学测量. 如果能量是量子化的，那么只有当微波频率恰好等于通过量子力学计算出的两个能级之间的能量差时，系统才会吸收光子并从低能级跃迁到高能级. 在实验上，他们固定一个2 GHz的微波，通过调节偏置电流大小来调能级，当能级差正好撞上2 GHz时就会出现一个吸收峰，他们前后观测到了3种不同跃迁的吸收峰. 这种共振吸收谱线证明了宏观相位δ的能量结构是离散的、量子化的. 这两项划时代的实验发现，有力地证明了人类可以在宏观尺度上设计和操控具有量子特性的系统，从而为量子信息科学的应用奠定了至关重要的基础.

3

量子计算与未来展望

约翰·克拉克、米歇尔·H·德沃雷和约翰·M·马蒂尼斯关于宏观量子效应的开创性工作，不仅是基础物理学原理上的巨大胜利，更是奠定一切基于超导电路的量子技术科学基础的里程碑。他们的研究成果直接催生了从精密测量到量子计算的跨越式发展。诺贝尔奖的核心实验平台——偏置约瑟夫森结——是实现宏观量子变量可控的电路关键，它的成功开启了更多重要的超导量子器件的诞生。值得强调的是，三位获奖人员在完成本次诺贝尔物理奖对应的开创性成果后，仍长期系统地致力于相关领域的后续研究。例如，约翰·克拉克教授的工作重心在于利用约瑟夫森结的极致灵敏度进行精密测量。事实上，在本次诺奖成果相关的关键发现之前，他就长期致力于推动超导量子干涉仪（SQUID）的发展。SQUID是利用两个并联的约瑟夫森结构建的超导环路，能够感应到极其微小的磁通量变化。它正是利用宏观量子相位的相干性，成为了目前世界上最灵敏的磁场探测器之一，广泛应用于地球物理学、生物磁测量和基础物理实验中。SQUID是宏观量子相干性走向实用化的早期典范。此外，克拉克教授在低温下闪烁噪声特性研究和抑制方面也取得了重大成果，为所有需要极高信噪比的量子实验提供了关键技术支持^[9].

三位科学家的工作证明了被束缚在势阱中的约瑟夫森相位δ具有离散的、可控的能级. 这使得科学家能够将这个宏观电路系统视为一个人造的“宏观原子”, 利用其最低的两个量子能级（基态和第一激发态）来承载和处理量子信息, 从而构造出超导量子比特（superconducting qubit）. 最初的超导量子比特设计面临着易受环境噪声干扰（即量子退相干）的问题，相干时间只有10 ns量级. 2001年，中国科学家韩思远和于扬等人系统性研究了约瑟夫森结中这种相干性为何以及如何消失，精确测量并量化了由耗散引起的退相干速率，这项工作为后续的量子比特设计（如Transmon的发展）提供了关键的实验数据和理论验证，指导了科学家们如何通过降低耗散来有效延长量子比特的相干时间^[10]. 2007年，Koch等人^[11]与游建强教授^[12]等研究者各自独立地提出了通过额外电容优化超导量子比特的方案, 其中最具代表性的便是Transmon量子比特^[11]. Transmon通过增大电容来降低对电荷噪声的敏感性, 显著地延长了量子比特的相干时间. 超导量子比特的相干时间已达毫秒量级^[13,14], 为构建实用量子计算机提供了坚实的物理基础. 而现代超导量子计算机操作的基础理论框架，正是德沃雷教授与合作者共同建立的电路量子电动力学（cQED)^[15]. Transmon量子比特的诞生也得益于他对超导量子比特设计优化上持续的工作.

超导量子计算已成为当前量子技术领域最主流和最具竞争力的技术路线之一, 近年来取得了多个里程碑式的成就. 2019年, 马蒂尼斯带领的谷歌团队宣布, 其基于53个超导量子比特的Sycamore芯片, 在特定计算任务上的速度超越了当时最强大的超级计算机^[16]. 而到2024年, 谷歌团队更是凭借配备105个高保真度量子比特的Willow芯片, 在硬件规模上实现翻倍的同时, 完成了低于阈值的量子错误校正演示, 证明了其芯片设计和技术能够有效抑制错误, 朝着构建大规模容错量子计算机迈出了关键一步^[17]. 有趣的是，马蒂尼斯于2020年离开谷歌，而2023年，德沃雷则加入谷歌开始领导量子团队. Sycamore和Willow两代芯片的开发，恰好体现了两位诺奖得主对量子计算工程化进程的接力式领导. 与此同时, 中国科学技术大学朱晓波、潘建伟团队也持续推进超导量子计算的进程, 并于2024年发布了其最新一代“祖冲之三号”超导量子计算原型机, 该机大大提升量子比特数量的同时, 各种硬件指标也达到了与谷歌Willow相近的水平^[18]. 此外, 国外的IBM等团队不断致力于量子计算机的商业化和工程化, 持续发布拥有数百甚至上千量子比特（如Condor芯片）的超导量子处理器, 并构建了基于云服务的量子生态系统；而诸如北京量子信息科学研究院等国内科研机构则在量子比特的制备、操控和量子纠错理论方面持续攻关, 共同推动着超导量子计算技术的快速成熟.

除了在超导器件领域取得的巨大成功, 这项诺贝尔奖所确立的宏观量子效应研究范式也极大地激励了其他宏观量子物理体系的快速发展. 例如, 2005年, 来自德国海德堡大学的科学家们使用超冷原子气体, 成功实现了一个宏观的一维双势阱模型^[19], 他们通过调节两个势阱之间偏置的势能差, 也成功观察到了隧穿现象, 甚至成功实现了玻色原子版本的约瑟夫森效应. 此外, 调节两个阱能量一致时, 能产生宏观量子叠加态. 在光力学系统（cavity optomechanics）中, 科学家也成功地将毫米级乃至更大尺寸的机械振子冷却至量子基态, 并利用光子与机械振子的耦合, 实现了大规模的、具有明确宏观质量的量子叠加态^[20], 也就是著名的“薛定谔的猫态”（Schrödinger's Cat State）.

在此基础上, 各种新奇的宏观叠加态也被设计出来并开始实验验证. 比如, 笔者之一于2016年与合作者提出的“薛定谔的细菌”方案^[21], 该方案在理论上探索了如何将一个宏观生命体（如细菌）的运动状态与超导电路中冷却到量子基态附近的宏观力学振子系统耦合, 通过超导量子比特调控使其质心运动进入量子叠加态. 而在这个方案中所需要用到的超导量子器件, 起源正是三位诺奖得主诺奖工作中所发展出来的. 近年来, 宏观力学振子系统的量子叠加态也促进人们探索引力场量子叠加, 以及引力量子效应诱导的量子纠缠, 这将会对量子力学与引力理论的统一带来新的视角^[22].